低信噪比运动红外点目标的检测
为解决高空背景条件下红外低信噪比运动点目标的检测问题,本文提出了一种基于膨胀累加的检测方法.运用形态膨胀运算能够使同一目标处于不同帧上的能量仍然能够实现有效的累加,从而达到目标增强的目的.同时本文还采用小波变换预处理的方法,对图像中相关的1/f噪声进行白化.本文对这一方法进行了大量的仿真实验和详细的理论分析.实验证明该算法能够快速稳定地检测出信噪比为2的运动点目标.
一、引 言
在红外寻的制导过程中,需要能够尽快地截获并锁定跟踪目标,由于红外传感器与目标之间的距离很远(通常为几十公里甚至上百公里),目标在像平面上的成像仅为点目标,并且淹没在各种杂波背景中.通常的点目标的检测方法采用多帧累加来提高信噪比,这种简单的累加方法在目标帧间移动很小时可以有效地抑制噪声并起到增强目标的作用.但对于运动速度较大的目标(平均几帧图像移动一个象像素),这种简单的累加方法并不能够实现有效的能量积累,很难检测出低信噪比并处于快速运动中的点目标.
为解决高空背景中低信噪比运动点目标的检测问题,本文提出了一种基于膨胀累加、检测前跟踪的算法.将经过白化预处理的图像作形态膨胀运算之后再进行累加,这样仍然可以使同一点目标在不同帧上的能量累加到同一像素点上,起到突出目标的作用.边检测边跟踪利用目标候选点在连续帧上的信息剔除虚警假目标,采用航迹关联判决的方法来提高算法的抗干扰性能.
本文采用红外线列扫描图像序列对算法进行模拟. 红外线列扫描图像主要有两种噪声:图像平面上的白噪声和线列扫描方向上的非平稳1/f噪声.本文采用小波变换的方法对线列扫描方向上的1/f噪声进行白化预处理.实验证明,该算法获得了很好的预处理效果.膨胀累加算法能够快速检测出信噪比为2的点目标.
二、低信噪比运动点目标的检测算法
1.图像预处理
高空背景可近似看作均匀辐射背景,传感器的内部噪声将起主要作用.在线列红外图像中主要存在不相关的白噪声和线列扫描方向上相关的1/f噪声.可以合理地把噪声看作加性噪声,图像序列可用下面的模型来表示:
x(i,j,t)=hδ(i-it,j-jk,t)+fn(i,j,t)+
(i,j,t) (1)
这里目标被看作位于点(it,jt)处幅度为h的冲激函数,图像预处理就是对1/f噪声fn(i,j)去相关.实际上,1/f噪声是一种统计自相似的分形随机过程[1].小波变换方法能够刻划分形过程的精细结构,对于非平稳过程的分析具有一定的优越性.因此本文采用这一方法对噪声进行白化处理.
小波变换将信号在一个由小波函数ψ(t)的整数平移和尺度伸缩所构成的规范正交基上展开,对于信号x(t),它能够用小波正交基来表示,同时还可由其小波变换系数来恢复:
xmn=∫+∞-∞x(t)ψmn(t)dt (2)
(3)
{xmn}即为x(t)在平移伸缩系{ψmn(t)}上的小波变换,对于二进小波变换,小波基函数可表示为:
ψmn(t)=2m/2ψ(2mt-n) (4)
文献[1]中提出了一种基于小波变换的1/f噪声表示方法,并证明了1/f噪声的小波变换系数可近似地看作彼此互不相关,通过各个尺度上方差的规一化,就能够对1/f噪声进行白化.对于1/f噪声信号x(t),其小波变换系数的方差具有如下形式:
Var[xmn]=σ22-γm (5)
其中γ为1/f噪声的功率谱参数.由于小波变换系数近似互不相关,小波变换系数可以用下式表示:
xmn=[σ2-γm/2]υmn (6)
其中小波变换系数υmn为零均值,单位方差并且互不相关的随机变量,它对应着一个平稳的白噪声υ(t),如果用(σ2-γm/2)-1对xmn归一化,就能够通过重构方程(3)得到一个白化的随机过程.
由于红外线列扫描图像只在扫描方向存在1/f噪声,为减少计算量,只考虑扫描方向的白化,这样可以只进行一维的处理,考虑到加性的白噪声,线列扫描序列的小波变换系数的方差为:
Var(xmi,j)=σ22-γm+σ2
(7)
其中σ2
为白噪声的方差,经(σ22-γm+σ2
)-1/2对小波变换系数xmi,j尺度化后,再用式(3)进行信号重构,就能够实现线列扫描方向的白化.通过上述的推导,可以得知预处理后的输出为零均值,单位方差的白噪声过程.
2.膨胀累加平均
当目标在帧间移动很小时,直接采用多帧图像累加的方法可以有效地抑制噪声,提高信噪比.但是帧间运动较大的点目标,直接累加并不能够实现目标能量的有效积累.在本文中,首先对图像进行膨胀运算,将目标由一个点膨胀成一个斑点,从而使得不同帧上的目标能量仍然能够实现累加,起到目标增强的作用.结构函数g(x)对函数f(x)的膨胀运算记为
,它可以由下式计算:
(8)
其中D(g)表示结构函数g(x)的定义域,进一步可以得到二维膨胀运算:
(9)
本文选择平顶形的结构函数,即对于所有(x,y)∈D(g),都有g(x,y)=1成立,此时某一个像素点的膨胀运算结果相当于以该点为原点的结构函数窗口内的所有像素灰度的最大值,则有:
(10)
其中结构函数尺寸大小根据目标在帧间运动的大小来选取.累加平均后的图像可表示为:
(11)
其中N为累加帧数,经N帧累加平均后,目标点和噪声点的均值保持不变,而均方差变为单帧时的1/N.最后将累加的结果取门限即得到一组目标候选点.
3.数据关联与检测判决
数据关联采用最近邻关联方法将目标候选观测点连成多条航迹.把每一次累加输出后的目标候选点视为一组,在得到T组连续候选点后,如果某一个目标航迹中的观测点数不少于S个,判决该航迹为目标航迹.假设第i条航迹观测数为nc(i)个,检测判决即为如下的判决过程:
(12)
三、模拟实验结果
图(1)给出了原始的红外线列扫描图像,从图像中可以看到图像在列方向(扫描方向)具有很强的相关性.图(2)为经小波变换预处理后的图像,图像列方向上的相关性得以滤除,图(3)为图像经膨胀累加取平均的结果,从中可以看到目标得到增强,图(6)为最终检测判决结果.实验证明该算法能够有效地检测出信噪比为2的运动点目标.


图1 红外线列扫描图像图2 经预处理后的图像


图3 膨胀累加平均后的图像图4 阈值化后的图像


图5 候选点航迹图6 检测结果(目标航迹
四、算法检测性能分析
首先假定噪声是均值为零,方差为σ2的高斯白噪声.为分析方便起见,假定目标为能量固定的冲激信号,幅度为m,令p0(x)和p1(x)分别表示噪声点和目标点灰度的概率密度函数
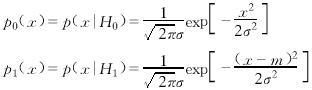
(13)
并令噪声点和目标点灰度值的分布函数分别为P0(x)和P1(x).下面讨论fd(x,y)中像素灰度的概率密度函数.由概率论的知识可知,两个相互独立的随机变量的最大值的分布函数为两个分布函数之乘积.令膨胀窗口的面积为M,如果某一个像素点的膨胀窗口内不包含目标点,则膨胀运算后该点灰度的分布函数为:
Pd,0(x)=PM0(x) (14)
对式(14)求导数,得到:
Pd,0(x)=Mp0(x)PM-10(x) (15)
同样可以得到像素点的膨胀窗口内包含有目标点时,膨胀运算后该像素的灰度概率分布函数和概率密度函数分别为:
Pd,1(x)=P1(x)PM-10(x) (16)
pd,1(x)=p1(x)PM-10(x)+(M-1)p0(x)P1(x)PM-20(x) (17)
实际上,累加平均的过程可以看作先将fd(x,y,k)除以N,再进行相加的过程.假定帧间没有相关性,我们知道,相互独立随机变量之和的概率密度函数为随机变量的概率密度函数之卷积.则累加平均后,噪声点和目标点的灰度概率密度函数为N次自卷积的结果:
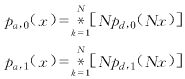
(18)
从上式可以看出,膨胀累加平均后的灰度概率密度函数的表达式十分复杂.本文采用近似方法计算pa,0(x)和pa,1(x),令膨胀累加后目标点和噪声点的灰度分别为高斯分布N(μ1,σ21)和N(μ0,σ20),对于累加平均判决门限Ts,其相应的检测概率PD,a和虚警概率PF,a为
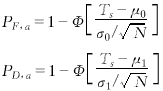
(19)
这里Φ[.]为标准正态分布的分布函数.
首先来计算膨胀运算后噪声点的均值和方差,μ0和σ20可以用下式求出:
μ0=σμmax(M)
σ20=σ2σ2max(M) (20)
这里μmax(M)和σ2max(M)为M个相互独立且服从标准正态分布的随机变量的最大值的均值和方差
μmax(M)=∫∞-∞Mxφ(x)ΦM-1(x)dx (21)
σ2max(M)=∫∞-∞M[x-μmax(M)]2Φ(x)ΦM-1(x)dx (22)
对于目标点,通过概率密度函数pa,1(x)计算目标点处膨胀运算后的均值和方差是不容易的.将目标膨胀窗口内的像素点的灰度写成{x1,x2,…,xM}的形式,不妨假设x1为目标点的灰度,则
max{x1,x2,…,xM}=max{x1,max{x2,…,xM}} (23)
令xm=max{x2,…,xM},由式(20)可知,xm的均值和方差为σμmax(M-1)和σ2σ2max(M-1).则目标点的均值和方差可表示为:
μ1=E[max(x1,xm)]
σ21=Var[max(x1,xm)] (24)
文献[4]中给出了一种计算两个正态分布的随机变量的最大值的均值和方差的计算方法,我们直接引用它来计算μ1和σ21:
(25)
其中
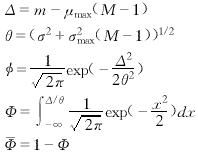
(26)
在图(7)中给出了背景噪声为零均值单位方差的白噪声、膨胀窗口取为2×2时PF,a和不同信噪比条件下PD,a随分割阈值的变化曲线.图(8)为信噪比取2、选取不同尺寸的膨胀窗口时(w×w),检测概率PD,a和虚警概率PF,a随分割阈值的变化曲线.从中可以看出,PD,a随膨胀窗口大小的变化并不明显,而PF,a则随着膨胀窗口的增大而迅速增加.因此选取的窗口太大,会降低检测性能.

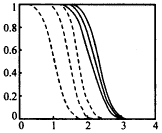
图7 PF,a和PD,a随分割阈值Ts的关系曲线(曲线附近的数字表明信噪比)图8 SNR=2时不同的膨胀窗口下的PF,a和PD,a(虚线表示PF,a,实线表示PD,a;
从左到右,w=2,3,4)
下面讨论关联后的检测性能.设膨胀累加门限化后的虚警概率为PF,a,目标检测概率为PD,a,航迹关联窗口取为[-nK,nK]×[-nK,nK],令K=(2nK+1)2,则对于虚警航迹,在关联窗口内有后续观测的概率为:
Pz,0=1-(1-PF,a)K (27)
由上式可以看出,虚警概率PF,a不宜取得较大,因为这样将会使虚警点在关联窗口内获得后续观测,从而增加整个检测算法的虚警概率.由于不同帧间的观测是相互独立的,因此航迹中的检测点的数目服从二项分布,包含t个检测点的航迹发生的概率为
.当某航迹中的观测数不小于某个值S,即认为该航迹为目标航迹.则虚警概率
(28)
考虑检测概率的计算.由于目标可能被分割出来,也有可能被阈值化为零,因此目标航迹的后续检测点可能为点目标,也有可能为关联窗口内的虚警点,仿照式(27),可得窗口内除点目标以外其余(K-1)个噪声点非零的概率为:
Pz,0,K-1=1-(1-PF,a)K-1 (29)
此时点目标的检测点-航迹关联,会有四种情况发生
(1)关联窗口内只有点目标,发生的概率为PD,a(1-Pz,0,K-1);
(2)关联窗口内存在点目标和噪声虚警点,发生的概率为PD,aPz,0,K-1;
(3)关联窗口内只有噪声虚警的情况,发生的概率为(1-PD,a)Pz,0,K-1;
(4)关联窗口内既没有点目标,也没有噪声点,发生的概率为(1-PD,a)(1-Pz,0,K-1).
在前三种情况下,目标航迹都会有后续检测点,则目标航迹有后续检测点的概率为:
Pz,1=PD,a+(1-PD,a)Pz,0,K-1 (30)
目标检测概率为:
(31)
航迹正确关联包括前两种情况,因此航迹正确检测的概率,即不包含噪声点的航迹检测概率为:
(32)
对SNR=2,N=5,膨胀窗口取为2×2,关联窗口为5×5时,在不同的PF,a值条件下,整个算法的检测概率PD和虚警概率PF与航迹判决阈值S之间的关系进行了分析计算(限于篇幅,不一一给出).发现PF,a的值取在0.002和0.005之间比较合适.这样选择主要出于两方面的考虑:一是此时检测概率和航迹正确概率很接近,更重要的是此时具有较高概率PD,a,这对于航迹的正确关联是十分重要的.图(9)给出了当PF,a=0.005、T=12时,整个算法的检测概率PD、PT和虚警概率PF与航迹判决阈值S之间的关系.
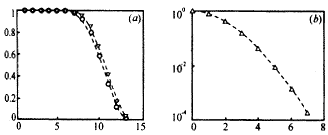
图9 PF,a=0.005时的检测概率和虚警概率 (a)三角点线表示PD,圆点线表示PT;(b)虚警概率PF
五、总 结
本文提出了一种膨胀累加、检测前跟踪的低信噪比运动目标检测算法,并采用小波变换的方法对图像进行预处理.模拟实验结果表明该算法能够检测出在帧间作快速运动的低信噪比点目标,实验取得了很好的实验效果,膨胀累加有效地克服了目标的帧间运动对多帧累加效果的不利影响.同时该算法计算量小且容易硬件并行实现,对于运动小目标的检测具有一定的实际应用价值.

