0 引言
输电线路行波故障测距技术因具有测距精度高和适用范围广等优点,一直为继电保护专业人员所关注[1]。早在20世纪50年代,国外就研制出A、B、C、D等4种基本型式的行波故障测距装置,但因存在可靠性差、构成复杂以及价格昂贵等问题,终究没有得到推广应用。
20世纪80年代,国内外在A型早期行波故障测距原理的基础上,提出了集保护和测距为一体的行波距离保护原理[2,3]。但由于测距算法不可靠以及现场试验条件的限制,行波距离保护没有得到进一步的发展。
20世纪90年代,我国提出了利用电流暂态分量的输电线路行波故障测距原理、算法及其实现方案[4-8],从而推动了现代行波故障测距(MTWFL)技术的发展[9],并相继研制出集A、D、E等多种原理的现代行波故障测距装置和系统,其绝对测距误差已经能够达到200 m以内 [10,11]。在应用研究领域,为了进一步提高行波故障测距的精度,小波模极大值检测理论已经被越来越广泛地用于单端和双端行波故障测距研究[12-15]。
近年来,国内学者开始将A型现代行波故障测距原理用于继电保护,并提出了基于小波变换的测距式行波距离保护原理[16,17]。
为了将A型现代行波故障测距原理更好地用于实测波形分析,本文将其划分为3种独立的运行模式,即标准模式、扩展模式和综合模式,并给出了各自用于实测电流暂态波形分析的典型实例。
1 A型现代行波故障测距原理的运行模式
A型现代行波测距原理为单端原理。根据所检测反射波性质的不同,可以将A型现代行波测距原理分为3种运行模式,即标准模式、扩展模式和综合模式。在标准模式下需要检测故障点反射波,在扩展模式下需要检测对端母线反射波,而在综合模式下则需要检测第2个反向行波浪涌并识别其性质。
1.1 标准模式
标准模式下的A型现代行波故障测距原理利用线路故障时在测量端感受到的第1个正向行波浪涌与其在故障点反射波之间的时延计算测量点到故障点之间的距离,其基本原理与早期的A型行波故障测距原理相同。为了实现标准模式下的A型现代行波故障测距原理,在测量端必须能够准确、可靠地检测到故障引起的第1个正向行波浪涌在故障点的反射波。
1.2 扩展模式
扩展模式下的A型现代行波故障测距原理利用线路故障时在测量端感受到的第1个反向行波浪涌与经过故障点透射过来的故障初始行波浪涌在对端母线反射波之间的时延计算对端母线到故障点之间的距离。
为了实现扩展模式下的A型现代行波故障测距原理,在测量端必须能够准确、可靠地检测到经故障点透射过来的故障初始行波浪涌在对端母线的反射波。
当故障点对暂态行波的反射系数较小时,在测量端可能检测不到本端第1个正向行波浪涌在故障点的反射波,从而导致标准模式下的A型现代行波故障测距原理失效。但在这种情况下,扩展模式下的A型现代行波故障测距原理却能很好地发挥作用。
1.3 综合模式
综合模式下的A型现代行波故障测距原理利用线路故障时在测量端感受到的第1个正向行波浪涌与第2个反向行波浪涌之间的时延计算本端测量点或对端母线到故障点之间的距离。
分析表明,无论母线接线方式如何,故障初始行波浪涌到达母线时都能够产生幅度较为明显的反射波[4]。可见,当线路发生故障时,测量端感受到第1个正向行波浪涌和第1个反向行波浪涌的时间是相同的。测量端感受到的第2个反向行波浪涌既可以是第1个正向行波浪涌在故障点的反射波(当故障点位于线路中点以内时),也可以是经过故障点透射过来的故障初始行波浪涌在对端母线的反射波(当故障点位于线路中点以外时),还可以是二者的叠加(当故障点正好位于线路中点时)。对于高阻故障(故障点反射波较弱),即便故障点位于线路中点以内,在测量点感受到的第2个反向行波浪涌也有可能为对端母线反射波。对于故障点电弧过早熄灭的故障(故障点不存在反射波),无论故障点位置如何,在测量点感受到的第2个反向行波浪涌均为对端母线反射波。
因此,当线路故障时,如果在测量端能够正确识别所感受到第2个反向行波浪涌的性质,即可实现单端行波故障测距。具体说来,当第2个反向行波浪涌为本端第1个正向行波浪涌在故障点的反射波时,二者之间的时间延迟对应于本端测量点到故障点之间的距离;当第2个反向行波浪涌为对端母线反射波时,它与本端测量点第1个正向行波浪涌之间的时间延迟对应于对端母线到故障点之间的距离。
可见,为了实现综合模式下的A型现代行波故障测距原理,在测量端必须能够准确、可靠地检测到故障引起的第2个反向行波浪涌并识别其性质。
2 利用电流暂态分量实现A型行波测距原理的直接波形分析法
2.1 行波故障测距基本关系
从行波故障测距的角度,可以将母线分为两种接线类型[4],其中第1类母线连接有同一电压等级的多回线路,而第2类母线只连接有1回线路。电力系统中的绝大多数母线均为第1类母线。相对于来自线路MN方向的行波而言,测量端母线M的等效波阻抗等于该母线上除线路MN以外所有线路波阻抗和母线分布电容的并联阻抗。假定连接到母线M的所有线路具有相同的波阻抗,则可以将母线M对来自线路MN方向的电压暂态行波的时域反射系数KMR和时域透射系数KMT表示为:
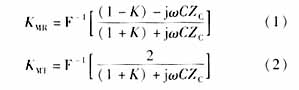
式中:F-1表示傅里叶反变换;K为除线路MN以外连接到母线M的线路回数(假定K≥2);C为母线M的分布电容;ZC为线路波阻抗。
假定M端电流正方向为母线到线路方向,则线路MN故障产生的初始行波浪涌到达本端时所引起的本线路电流暂态故障分量可以表示为:

M端第1个正向行波浪涌eF(t)(即故障初始行波浪涌在母线M的反射波)在故障点的反射波到达母线M时所引起的本线路电流暂态故障分量可以表示为:
式中:KFR为电压暂态行波在故障点的反射系数(假定为常数)。
故障初始行波浪涌在线路MN对端母线N的反射波透过故障点到达母线M时所引起的本线路电流暂态故障分量可以表示为:
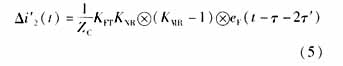
式中:KFT为电压暂态行波在故障点的透射系数(假定为常数);KNR为电压暂态行波在对端母线N的反射系数; 为暂态行波从故障点到对端母线N的传播时间。
比较式(3)~(5)可以得到:
暂态行波在母线M和故障点F的反射系数恒为负值,在故障点的透射系数恒为正值。因此,故障初始行波浪涌和故障点反射波到达母线M时引起线路MN的电流暂态故障分量Δi1(t)和Δi2(t)具有相同的极性,二者之间的时延等于暂态行波在M端测量点与故障点之间往返一次的传播时间。故障初始行波浪涌与其在故障线路对端母线N的反射波到达M端母线时引起的本线路电流暂态故障分量Δi1(t)与Δi′2(t)在某一初初始时段内(取决于对端母线N的接线方式)具有相反的极性[4],二者之间的时延等于暂态行波在故障点与对端母线N之间往返一次的传播时间。
可见,当线路发生故障时,通过比较来自故障方向的行波浪涌到达测量端母线时引起故障线路电流暂态分量的初始极性可以识别来自故障点和线路对端母线的反射波。在这种情况下,只要能够正确区分来自故障线路正方向和反方向的行波浪涌到达测量端母线时引起本线路的电流暂态分量,即可实现各种运行模式下的A型现代行波故障测距原理。
2.2 来自故障方向行波浪涌引起电流暂态分量的识别
来自故障方向任一点X的行波浪涌到达母线M时所引起的故障线路以及各相邻健全线路的电流暂态分量可以表示为:
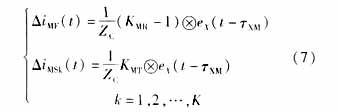
式中: 为暂态行波从X点到母线M的传播时间;K为相邻健全线路回数(设K≥2)。
由于反射系数KMR恒小于0,因此式(9)表明,来自故障方向的任一行波浪涌到达母线M时所引起的故障线路电流暂态分量和其它所有相邻健全线路电流暂态分量之间存在反极性的关系。
同理可知,来自任一线路正方向的行波浪涌到达母线M时所引起的该线路电流暂态分量和其它所有线路(包括故障线路)电流暂态分量之间存在反极性的关系。因此,通过比较行波浪涌到达母线M时所引起各线路电流暂态分量的极性即可识别来自故障方向行波浪涌所引起的电流暂态分量。
当母线上出线较多时,来自故障方向的行波浪涌到达母线时所引起各健全线路的电流暂态分量幅度很小,甚至可以忽略,从而简化了故障测距过程。
需要指出,在以上的分析中没有考虑线路损耗和线路参数的依频特性,这些影响因素将导致行波在传播过程中的衰减和畸变,但上述各行波浪涌之间的极性关系仍然成立。
2.3 直接波形分析法的实施步骤
利用电流暂态分量的直接波形分析法实现A型现代行波故障测距原理的具体步骤如下(以综合模式为例):
1)通过比较同母线上各线路电流故障暂态分量波形中第1个波头分量的极性选择故障线路;
2)对于故障线路电流暂态波形中的每一个波头分量,通过比较它与同一时刻其它线路电流暂态分量的极性确定来自故障方向行波浪涌引起的第2个波头分量;
3)通过比较来自故障方向行波浪涌引起的故障线路电流暂态波形中第2个波头分量与第1个波头分量的初始极性确定第2个波头分量是由故障点反射波所引起(二者同极性),还是由对端母线反射波所引起(二者反极性),进而确定故障点位置。
3 实测故障分析
3.1 本端和对端母线均为第1类母线
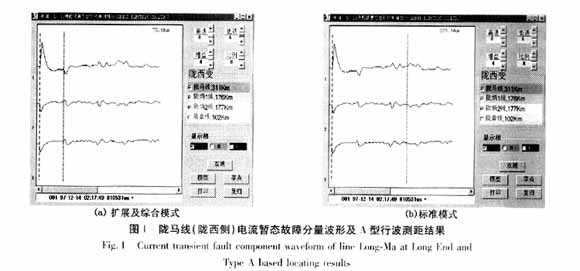
1997年12月14日2时17分49秒,甘肃天水供电局所管辖的330 kV陇马线(全长311 km)发生A相接地故障,其中陇西侧含故障线路在内同母线上3条线路的故障相电流暂态故障分量波形如图1所示。显然,本端母线为第1类母线。在故障线路上,来自故障方向行波浪涌引起的第2个波头分量与初始波头分量始终具有相反的极性,因而必为对端母线反射波所引起,而且对端母线也是第1类母线,从而可以直接获得扩展和综合模式下的测距结果为75.8 km,如图1(a)所示。标准模式下的测距结果可以间接获得(本例中难以直接获得),它应该等于故障线路实际导线长度与扩展或综合模式下测距结果之差值,并且可以近似表示为(km)。从故障线路电流暂态分量波形中可以发现,在对应于该近似测距结果的位置并不存在暂态波头分量,但在其邻域内距离本端235.6 km处存在由来自故障方向行波浪涌所引起的暂态波头分量,如图1(b)所示,从而可以将标准模式下的测距结果修正为235.6 km。实际故障点位于距本端(235~236)km处。在本例中,对端母线反射波先于故障点反射波到达本端测量点,因而故障点位于线路中点以外(靠近对端)。
2002年4月5日14时33分7秒,黑龙江绥化电业局所管辖的220 kV康绥甲线(全长64.3 km)发生B相接地故障,其中康金侧含故障线路在内同母线上3条线路的故障相电流暂态故障分量波形如图2所示。故障线路两端母线都连接有多条其它线路,故两端母线均为第1类母线。在故障线路上,来自故障方向行波浪涌引起的第2个波头分量与初始波头分量始终具有相同的极性,因而必为故障点反射波所引起,从而可以直接获得标准和综合模式下的测距结果为27.4 km,如图2(a)所示。在故障线路上,来自故障方向行波浪涌引起的第3个波头分量(叠加在暂态波形的第2个暂态分量上)与初始波头分量始终具有相反的极性,因而必为线路对端母线反射波所引起,从而可以直接获得扩展模式下的测距结果为36.9 km,如图2(b)所示。实际故障点位于距对端37 km处。在本例中,故障点反射波先于对端母线反射波到达本端测量点,因而故障点位于线路中点以内(靠近本端)。

3.2 本端和对端母线分别为第1类和第2类母线
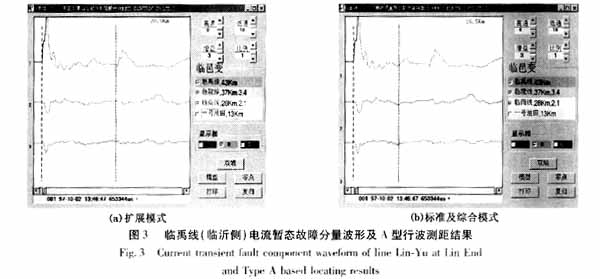
1997年10月2日13时46分47秒,山东德州电业局所管辖的110 kV临禹线(全长43 km)发生B相接地故障,其中临邑侧含故障线路在内同母线上3条线路的故障相电流暂态故障分量波形如图3所示,可见该波形较为复杂。仔细分析可以发现,在故障距离为26.9 km处存在由来自故障方向行波浪涌引起的波头分量,其初始极性与故障初始波头分量的极性相反,但二者很快变为同极性,因而必为线路对端母线反射波所引起,而且对端母线必为第2类母线,从而可以直接获得扩展模式下的测距结果为26.9 km,如图3(a)所示。标准和综合模式下的测距结果可以间接获得,并且近似为(km)。从故障线路电流暂态分量波形中可以发现,在对应于该近似位置的邻域内距离本端16.5 km处存在由来自故障方向行波浪涌所引起的暂态波头分量,如图3(b)所示,从而可以将标准和综合模式下的测距结果修正为16.5 km。实际故障点位于距本端16 km处(线路中点以内)。
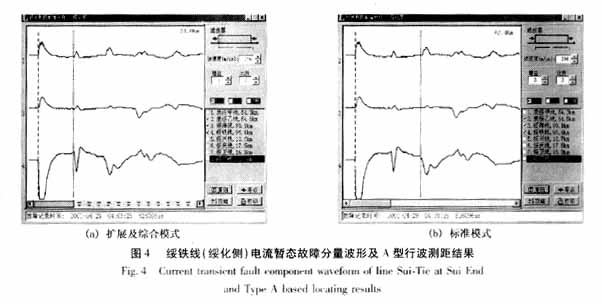
2001年4月29日4时3分25秒,黑龙江绥化电业局所管辖的220 kV绥铁线(全长96.4 km)发生A相接地故障,其中绥化侧含故障线路在内同母线上3条线路的故障相电流暂态故障分量波形如图4所示。在故障距离为34 km处存在由来自故障方向行波浪涌引起的2个波头分量,其初始极性与故障初始波头分量的极性相反,但二者很快变为同极性,因而必为线路对端母线反射波所引起,而且对端母线必为第2类母线,从而可以直接获得扩展和综合模式下的测距结果为34 km,如图4(a)所示。在故障距离为62.4 km处存在由来自故障方向行波浪涌引起的第3个波头分量,其极性与故障初始波头分量的极性始终相同,因而必为故障点反射波所引起,从而可以直接获得标准模式的测距结果为62.4 km,如图4(b)所示。实际故障点位于距本端62.525 km处(线路中点以外)。
4 结语
本文将A型现代行波故障测距原理划分为标准、扩展及综合等3种独立的运行模式,并通过利用电流暂态分量的直接波形分析法将各种运行模式用于实际故障产生的电流暂态波形分析。实测故障分析表明,A型现代行波故障测距原理的绝对测距误差不超过500 m。
由于有些故障暂态波形较为复杂,使得并非在所有运行模式下都能够直接获得可靠的测距结果。为了进一步提高A型现代行波故障测距原理的可靠性,结合实际故障暂态波形,深入研究实时、可靠的现代行波检测与识别算法是非常必要的。
