0 引言
电力变压器是电力系统的重要设备。随着电力系统规模的扩大,高电压等级线路的迅速增加,大容量、高电压的大型电力变压器大量投入运行,其安全运行更被人们所关注,对电力变压器继电保护装置准确动作提出了更高的要求[1-2]。
资料表明[3],220kv以上变压器保护的正确动作率平均为68.96%,远低于发电机保护的正确动作率98.2%和系统保护的正确动作率99.33%,而励磁涌流是引起变压器误动的一个重要因素。因此,有效地识别短路故障电流与变压器励磁涌流是继电保护中的重要研究课题。
目前在理论上进行过研究,并已经运用于实践的变压器励磁涌流识别方法可分为以下两类:1)利用变压器电流量判别励磁涌流,如间断角原理、二次谐波制动原理[1];2)同时利用变压器电流和电压量判别励磁涌流,如磁通特性原理和等值电路参数原理[1-4]。
二次谐波制动原理是通过计算差动电流中的二次谐波电流分量来判断是否发生励磁涌流。当出现励磁涌流时应有:Id2>KId1。其中,Id1、Id2分别为差动电流中的基波和二次谐波电流的幅值;为二次谐波制动比。但是,由于变压器磁特性的变化,某些工况下励磁涌流的二次谐波含量低,容易导致误动;而大容量变压器、远距离输电的发展,使得内部故障时暂态电流可能产生较大二次谐波,容易导致拒动。
间断角原理是根据变压器在励磁涌流和内部故障时电流波形所具有的不同特征来区分励磁涌流和内部故障的。但是,用微机实现间断角原理需要解决必须采用较高的采样率和较高的采样精度才能准确地测量间断角的大小,并正确判断电流是否进入“间断”范围的问题。同时还需要解决由CT传变引起的励磁涌流间断角的变形问题。这些问题对微机实现间断角原理的硬件复杂性和成本都提出了很高的要求。
等值电路参数鉴别法提出了一种基于变压器导纳型等值电路的参数鉴别方法,该方法同时利用了变压器的电压、电流量,通过检测对地导纳参数变化来鉴别变压器故障与否。但是,该方法需要获取变压器的漏电感参数,以求取对地导纳参数。
利用磁通特性鉴别励磁涌流是近期比较活跃的研究方向之一。已有的一些基于变压器磁通特性原理的鉴别方法需要准确的变压器参数或磁化曲线,而且这些量对于判别效果有很大影响。
本文提出了一种不需要变压器参数的磁通轨迹特征法来识别励磁涌流。该方法根据变压器发生内部故障时铁心不饱和,而出现励磁涌流时铁心饱和的原理,利用实测的变压器电压和电流量来推算变压器主磁通的轨迹,通过提取主磁通轨迹的特征来判断主磁通变化范围位于线性部分还是磁路饱和部分,从而确定变压器是否发生励磁涌流。仿真和实验结果表明,该方法能够快速、有效地识别变压器的励磁涌流和内部短路故障。
1 主磁通轨迹分析
设单相双绕组变压器物理模型如图1所示,其中i1、i2分别为原、副边绕组电流,u1、u2分别为原、副边绕组端电压,w1、w2分别为原、副边绕组匝数,Φm为主磁路磁通。

考虑变压器主磁路磁滞,主磁路磁通Φm与变压器原、副边的差电流Δi(Δi=i1-i′2,i′2为折算后的副边电流)的关系曲线如图2中虚线所示。差电流Δi即为变压器正常运行时的励磁电流。由于实际电路中所施加的电压为工频交流电压,变化较快,所以实际磁通轨迹通常达不到理想磁滞回环两端比较尖的部分,而是如图2中实线所示。由于主磁路中存在磁滞和涡流损耗,使得主磁通的变化在时间轴上总是落后于励磁电流。这样,在主磁通未进入饱和区的情况下,则主磁通和励磁电流都是随时间的正弦变化量,且二者之间存在一个相位差。因此,Φm-Δi的轨迹曲线近似为一个椭圆,如图3(a)所示;而当变压器发生励磁涌流时,主磁通周期性地进入和退出饱和区,并且磁通和励磁电流中的自由分量使得Φm-Δi轨迹偏向一侧,如图3(b)所示.
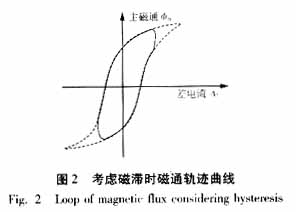

从Φm-Δi轨迹曲线的特征可以很明显地判别出变压器铁心是否饱和,从而判断出是否发生了励磁涌流。
下面,我们以图1所示的单相双绕组变压器为例,分析如何得到主磁路磁通对于原、副边差流的关系曲线。
对于图1所示的变压器物理模型,其电路方程为:

其中,r1,r2分别为原、副边绕组的电阻;L1,L2分别为原、副边绕组的漏感,分别对应于漏磁通Φs1、Φs2。
变压器空载时,副边电流为零,(2)式为

Φ0为变压器铁心的剩磁,是一常量。从数值的角度看,其大小只影响Φm-Δi曲线的上下平移,并不影响其形状,因此不影响对Φm是否进入饱和区的判断。设Φ0=0,则(3)式变为:
所以,变压器空载时,用(5)式即可求得变压器的主磁通;变压器带负载时,尽管用(5)式求得的磁通Φ为主磁路磁通Φm的近似值,但它们具有相似的特征。因此,不论变压器带负载与否,都可由(5)式求得的主磁通Φm。
变压器发生内部短路故障时,一般将短路部分看作第三绕组,相当于一台三绕组变压器在第三绕组发生短路,其等效电路图如图4所示。

其中
分别为折算后短路绕组电阻和漏感,r′2、L′2别为折算后的副边绕组电阻和漏感。此时,原边电流与折算后副边电流之差为正常运行时励磁电流与流过短路绕组的电流之和,即Δi=i1-
,其中i0为变压器正常运行时的励磁电流。此时差电流Δi被称为等效励磁电流。由于存在短路部分的损耗,相当于的主磁通Φm滞后等效励磁电流的角度增大,Φm-Δi轨迹椭圆的长、短轴比例缩小。短路匝数越多,则损耗越大,椭圆的长、短轴比例也越小,甚至发生反转。
2 励磁涌流的磁通轨迹特征
选择和提取特征是区分变压器励磁涌流和内部短路故障过程中的一个关键问题。由于发生励磁涌流时,主磁通交替经历进入和退出饱和区的过程,则对于正方向的励磁涌流,在电流最大点imax附近,主磁通严重饱和,该处附近的磁通轨迹曲线与横轴的夹角α近似为0°;在电流最小值imin附近,磁通退出饱和,该处附近的磁通轨迹曲线与横轴的夹角β近似为90°,如图3(b)所示;而对于反方向的励磁涌流,情形刚好相反。但在变压器发生内部故障时,磁通变化范围始终处于非饱和区,磁通轨迹曲线与横轴的夹角在电流最大值与最小值附近基本相同,即α≈β,如图3(a)所示。根据这一特点,我们提出采用最大、最小励磁电流处磁通轨迹曲线倾角的正弦值之差作为区分励磁涌流与内部故障的特征指标。定义特征指标:
k的取值范围为0≤k≤1。显然,对于励磁涌流,由于α与β相差较大,测算出的k值将接近于1。而对于内部故障,由于α≈β,测算出的将接近于0。
应当注意的是,在最大、最小励磁电流处磁通轨迹曲线的倾角通常经历了一个较大的变化过程,因此直接采用磁通轨迹曲线局部的微分或差分计算倾角α和β存在数值不稳定问题。类似的问题在一些基于dΨ/di的方法中也常会遇到。为此,我们需要将倾角α和β理解为最大、最小励磁电流附近相对较宽时间范围内磁通轨迹曲线的平均倾角,例如,这个时间范围可以取到1/10周期。我们将该时间段内的所有采样数据点(Φm,Δi)拟合为一条直线,然后以该直线的倾角作为磁通轨迹曲线的平均倾角。
区分励磁涌流与内部故障的判据为:如果k>kcr则判为励磁涌流,否则判定为内部故障。其中kcr是一个由用户整定的临界值。通常情况下可设置为0.5。
3 仿真验证
我们利用EMTP仿真程序对单相变压器励磁涌流与内部故障进行了仿真研究,并用这些仿真数据绘制了磁通轨迹图,计算了励磁涌流与内部故障的特征指标。
单相变压器空载合闸与空载匝间短路故障仿真波形分别如图5(a)、6(a)所示,其相应的磁通轨迹曲线如图5(b)、6(b)所示。由于励磁涌流和短路电流的实际数值可能很大,为了比较和计算方便起见,对磁通轨迹图曲线进行归一化处理,即磁通轴和电流轴分别除以其最大值与最小值之差。把电流最大值、最小值之前0.002s内的所有数据点用一条直线拟合。分别计算电流最大值处的拟合直线与横轴夹角α的正弦值s1和电流最小值处的拟合直线与横轴夹角β的正弦值s2。


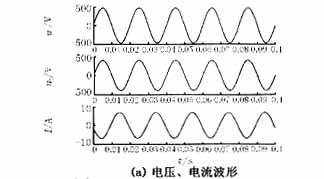

对于图5(a)中所示的空载合闸波形,求得s1=0.2417,s2=0.9982,k=‖s1|- |s2‖=0.7565;对于图6(a)中所示的空载匝间短路故障波形,求得s1=s2=0.9495,k=‖s1|-|s2‖=0.0。显然,按照k>0.5判据,可以很容易地识别出励磁涌流。
4 动模实验
下面用清华大学动模实验室的单相双绕组变压器实验数据,来验证识别方案以及设定的门槛值。该变压器的额定参数为:额定容量5kVA,额定电压460V/400V,原副边绕组匝数比为271/234。
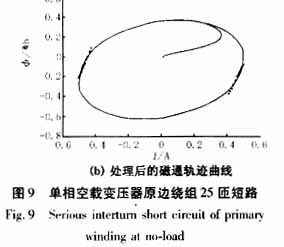
单相变压器空载合闸(励磁涌流)、小匝数匝间短路、大匝数匝间短路时的电压、电流波形以及经过处理后的磁通轨迹图分别如图7、8、9所示。多次实验均具有相似的波形。求得变压器八次空投实验(出现励磁涌流)时k的值均大于0.9332,均满足判据;求得变压器四次空载匝间短路故障(包括大匝数短路和小匝数短路)时k的值均小于0.0434,均不满足判据k>0.5。


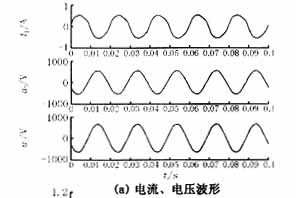
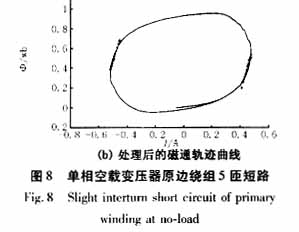

该识别方法不受剩磁大小的影响,判定时间比较短(用一个周期的时间即可完成判定)。而且,由于采用正弦值的绝对值计算判据,所得到的判据值在0-1范围内变化,与变压器电压、电流的实际值无关,便于统一整定。
5 结论:
本文提出一种不需要变压器参数的磁通轨迹特征法识别励磁涌流。该方法利用实测的变压器电压和电流量来推算变压器的主磁通轨迹,并按照主磁通轨迹的特征量来判断主磁通变化范围位于线性部分还是磁路饱和部分,从而确定变压器是否发生励磁涌流。该识别方法利用积分方法求取磁通,避免了微分带来的无穷值问题。其判据值在0-1范围内变化,与变压器的实际值无关,便于统一整定。而且判定时间短,不受剩磁大小的影响。仿真和实验结果表明,该方法能够快速、可靠地识别变压器的励磁涌流和内部短路故障。
