高频雷达抑制冲击干扰的研究与实验
工作在高频波段的超视距雷达如何抑制雷电、无线电通信等信号的冲击干扰是目前国内外尚未解决的问题.本文首次揭示了这种干扰在雷达多普勒域存在的奇异性特征,并根据这种特征提出了在多普勒域检测冲击干扰的小波分析方法和高频雷达抑制冲击干扰的方案.现场实验结果表明这种方法简便有效.本文从理论上解决了在窄带相关系统中检测冲击干扰的问题,工程上实现了高频雷达对冲击干扰的抑制,从而提高了这种雷达的生存能力.
一、引 言
高频雷达(High Frequency Radar)主要应用于超视距目标的探测[1],怎样抑制雷电、无线电通信信号对它造成的冲击干扰是一个受到广泛关注的问题.冲击干扰严重影响高频雷达检测信噪比,有时导致雷达不能正常工作.目前这个问题国内外尚未能解决.高频雷达属于窄带相关系统,它的系统带宽与信号带宽基本一致,由于冲击干扰信号在系统内部与回波信号占据同等的带宽,所以频谱分析方法不能将目标回波信号和冲击干扰加以区分,更不能抑制这种干扰.众所周知,小波变换理论是处理突变信号的有力工具,人们一直努力应用小波变换理论解决窄带相关系统中的冲击干扰问题,但是至今没有取得重大进展.其主要原因在于冲击干扰信号经过系统窄带平滑后失去了时间上的突变性质,系统记录的时域冲击信号已不再有明显的时域突变特征,因此用小波变换理论处理窄带系统内的时域信号显得毫无意义.窄带系统接收的冲击干扰是否真的失去了时间上的突变特征,如果没有失去这种特征,怎样利用小波变换理论进行检测成为了一个悬而未决的问题.
本文的理论分析揭示了这个问题的答案.通过提取、分析信号的多普勒信息,可以发现冲击干扰在信号的多普勒域仍然保留着明显的奇异特性征,这一特征是目标回波所没有的.根据冲击干扰的这一特点,本文提出了利用小波分析技术在回波信号的多普勒域中检测冲击干扰的方法,解决了窄带相关系统检测冲击干扰的问题,为高频雷达抑制雷电等信号的冲击干扰找到了理论依据,从而开辟了小波分析理论在窄带相关系统中应用的新途径.
二、冲击干扰在高频雷达多普勒域的奇异特征
高频雷达是窄带相关系统,采用距离门-多普勒信号处理方法.图1给出雷达系统的简单框图.
图1 高频雷达系统的简单框图
距离R处以速度v沿径向匀速运动的点目标P的回波信号表示为g(t)=f(t-τ0)ejωd(t-τ0).其中f(t)是雷达发射信号,
是距离延迟,c是光速,
是多普勒角频率,ωc=2πfc,fc是载频.雷达信号处理的数学表达式是
(1)
这一处理过程实际分为图1表示的几个步骤.点目标P的回波信号混频后得到的基带信号r(t)=s(t-τ0)ejωdt,s(t)=s(t-nTp)是发射信号的基带信号,n是整数,Tp是基带信号重复周期(扫频周期).第n个基带信号重复周期的距离处理公式是

(2)
当τ=τ0时,获得xn(τ)的最大值
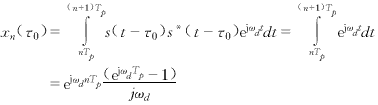
(3)
由式(3)知,距离处理的结果xn(τ0)是对目标P多普勒信号的采样,采样周期是Tp.对序列{xn(τ)}n∈[0,N-1]作离散傅立叶变换实现速度处理,获得距离单元τ的多普勒谱,即
(4)
由X(τ,m)可换算出目标的速度.式(4)表示的是信号由多普勒域至多普勒谱域的变换.
若在基带信号重复周期k至周期l的时间段上,系统受到总长为(l-k+1)Tp的冲击干扰,且用n(t)表示干扰通过系统前端后得到的基带信号.n(t)的距离处理应为n′n(τ)=
.由于n(t)是系统带内白噪声,s(t)有理想低通频率响应,那么n′n(τ)是低通白噪声,其带宽等于s(t)的带宽W.在任一距离单元τ上,由于高频雷达扫频周期
,可以认为n′n(τ)和n′n+1(τ)是不相关的.因此序列{n′n(τ)}n∈[k,l]中的元素彼此不相关.
由以上分析可知目标的多普勒信号序列{xn(τ)}n∈[0,N-1]与冲击干扰的多普勒序列{n′n(τ)}n∈[k,l]存在明显区别:(1)目标的多普勒信号持续分布在整个时间段上,冲击干扰仅存在于有限时段上;(2)目标的多普勒信号与目标运动状态有关,有确定的变化规律,一般是连续可导的,而冲击干扰的多普勒信号是奇异信号.
三、多普勒域小波分析方法检测冲击干扰的方法
上面的分析表明冲击干扰在高频雷达多普勒域表现出区别于目标信号的奇异性特征,这一特征是检测和判断干扰时间位置的根据.Mallat在文献[2]中提供了使用小波变换检测奇异信号的方法,这种方法不仅可以确定奇异信号的位置,而且可以定量求得信号的Lipschitz指数.文献[2]指出负Lipschitz指数信号的小波变换结果表现为:小波系数模值随尺度减小而增大.而正Lipschitz指数的信号则相反.依据这一规律可以检测负Lipschitz指数信号的位置.在本文研究中,冲击干扰{n′n(τ)}n∈[k,l]的Lipschitz指数显然是负数,回波信号{xn(τ)}n∈[0,N-1]的Lipschitz指数是正数.如果区分信号Lipschitz指数的正负,则不必过多考虑小波函数的消失矩.因此这里选择小波函数主要考虑小波函数是否有好的时间-频率局部性质,以及是否具有正交性.
根据高频雷达多普勒信号是复信号以及杂波能量集中在低频部分的特点,本文提出利用小波分析技术在多普勒域检测冲击干扰的具体方法.这种方法使用多分辨分析的快速算法式(5)实现小波变换[3].

(5)
式(5)中g(n)和h(n)分别是计算小波系数和尺度函数系数的滤波器,dj(n,τ0)表示尺度为2j时的尺度函数系数,cj(n,τ0)表示尺度为2j时的小波函数系数.图2给出相应的信号处理框图.多普勒信号的实部和虚部经过多分辨率分析,在不同尺度上得到各自的小波系数,构成新的复数序列.新序列的模与给定的门限进行比较,超过门限者被认为是存在冲击干扰的部分.

图2 小波分析检测冲击干扰算法框图
四、高频雷达抑制冲击干扰的原理
高频雷达回波的主要成分是海杂波,海杂波的一阶Bragg频率成分最强,因此高频雷达多普勒信号的主体近似于正弦信号,冲击干扰是叠加在这个信号上的奇异部分.为了抑制冲击干扰需要对雷达多普勒信号的奇异部分加以处理,处理的具体方法是把奇异部分从信号中剔除,然后用合理的数值填充剔除奇异信号后留下的空缺.利用前文给出的方法确定奇异信号的位置以后,可以方便地将干扰剔除,然而怎样用数据填补信号的空缺是需要研究的问题.冲击干扰位置的真实回波信号已被破坏,这部分数据必须人为产生,产生的数据越接近回波信号的真实值,雷达得到的信噪比改善越大.高频雷达多普勒信号的主体基本上是平稳的正弦信号,因此通过建立多普勒信号的线性预测模型[4]能对需要填补的部分进行预测,由这种方法得到的填充数据在理论上有充分的根据,在实践中获得了良好的效果.具体的建模和预测方法我们已在另一篇文章中讨论[5].
五、高频雷达抗冲击干扰实验
雷电对许多电子设备会造成强烈的冲击干扰[6、7],高频雷达一直没有有效的手段抑制雷电干扰.本文解决了高频雷达抑制冲击干扰的问题,为雷达抗雷电提供有效的手段.1997年9月按本文方法进行了高频雷达抑制雷电干扰的现场实验.下面列举实验的部分结果及分析.实验是在雷达附近地区上空有雷暴活动的条件下完成的,我们利用HP3585频谱分析仪监视了雷达工作频段的雷电信号.实验中将本文提出的算法插入到雷达距离处理与速度处理两个环节之间,处理了受雷电干扰的多普勒信号.下面是实验的结果和数据.
图3给出实验记录的高频雷达多普勒信号.其中虚线是某距离单元多普勒信号实部的一部分.易见170点至174点,285点至287点有明显的奇异信号(雷电干扰信号),其余类似正弦波信号的主要成分是海杂波.

图3 高频雷达多普勒信号实部
实验中按图2的方法提取了多普勒信号的小波系数模值,图4(a)、(b)分别给出了尺度1、2的小波系数模值.实验中使用的滤波器h(n)={0.542,0.307,-0.035,-0.078,0.023,0.030,-0.012,-0.013,0.006,0.006,-0.003,-0.002}.g(n)={0.542,-0.307,-0.035,0.078,0.023,-0.030,-0.012,0.013,0.006,-0.006,-0.003,0.002}
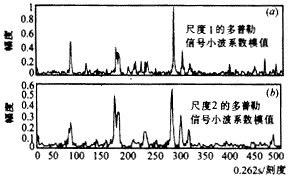
图4 不同尺度的多普勒信号小波系数模值
小波系数模值通过门限检测确定了雷电信号位置,既而将受雷电干扰的部分剔除,再由多普勒信号的线性预测模型产生预测信号对多普勒信号进行恢复,恢复后的信号实部在图3中用实线表示,可见信号的奇异部分已经被平滑的预测信号替代.目标信号强度低于海杂波20~30dB,在图3中很难分辨,需进行多普勒谱分析方可以检测.图5是高频雷达多普勒信号的谱分析.图5中虚线是干扰未被抑制时的多普勒谱分析结果,实线是干扰被抑制后的多普勒谱分析结果.图5表明雷电干扰被抑制后这个距离门的噪声基底平均降低了9.6dB,原来被噪声基底淹没的目标信号(在横坐标63点处)又可以检测.
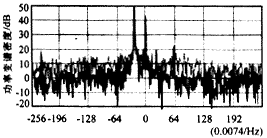
图5 冲击干扰被抑制前后的高频雷达多普勒谱分析结果
六、结 论
高频雷达抑制冲击干扰必须解决这样两个问题:(1)在窄带相关系统中找到冲击干扰的时间突变特征;(2)选用一种能够检测、处理突变信号的信号处理方法.本文解决了上述两个问题,并得到下面三个结论:(1)冲击干扰在窄带相关系统多普勒域表现出奇异性,这是区别冲击干扰信号与回波信号的基本特征.(2)在窄带相关系统多普勒域可以使用小波分析技术来实现奇异信号的检测,这个观点的提出开辟了小波变换在窄带相关系统中应用的途径.(3)高频雷达抗冲击干扰现场实验表明,本文提出的方法可靠有效,且易于工程实现,有重要的实际意义.

